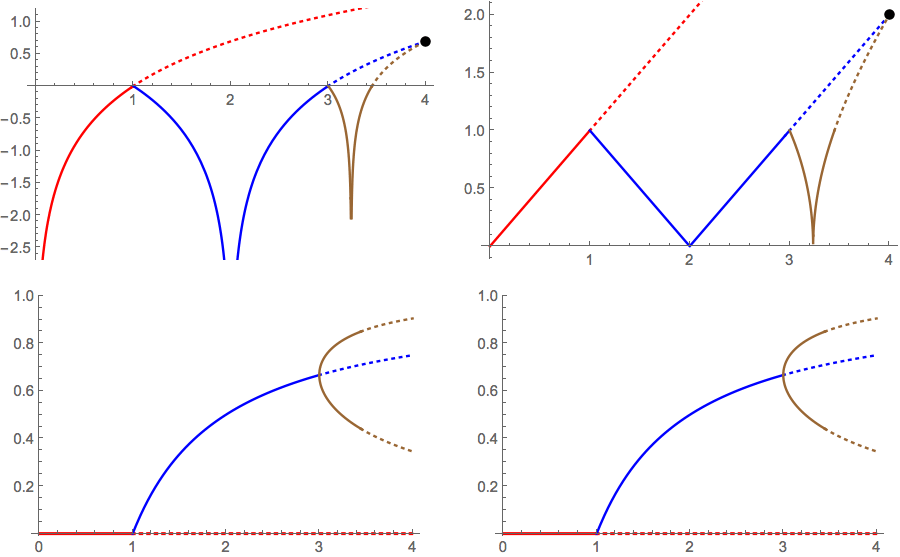
We start with what can be computed exactly. The upper left figure shows the Lyapunov exponent as a function of
a,
and the upper right figure shows the Lyapunov multiplier as a function of a.
The bottom diagrams both show a partial bifurcation diagram, the period 1 and 2 points as a function of
a. These figures were made with knownLiapunovExponents.nb

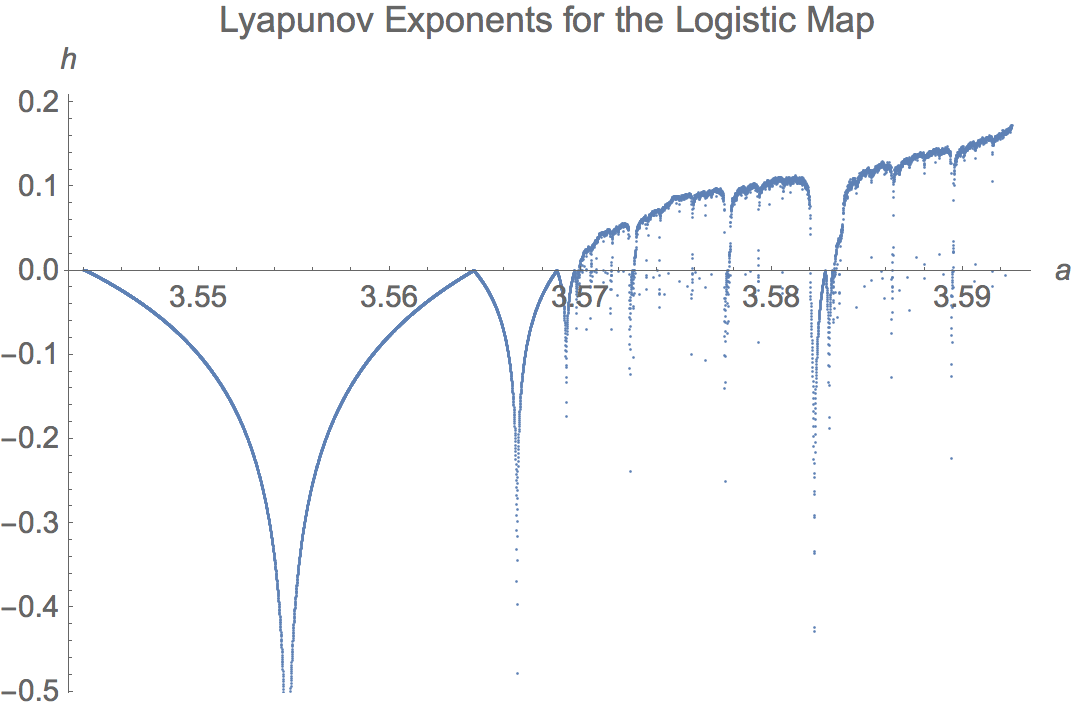
Now consider the graph of the Lyapunov exponent for the attractor (the orbit of 1/2 except when a = 4) computed numerically. These are computed
with computedLiapunovExponents.nb
Start with a in [3, 4], and then expand the interval twice about the accumulation of period doublings.
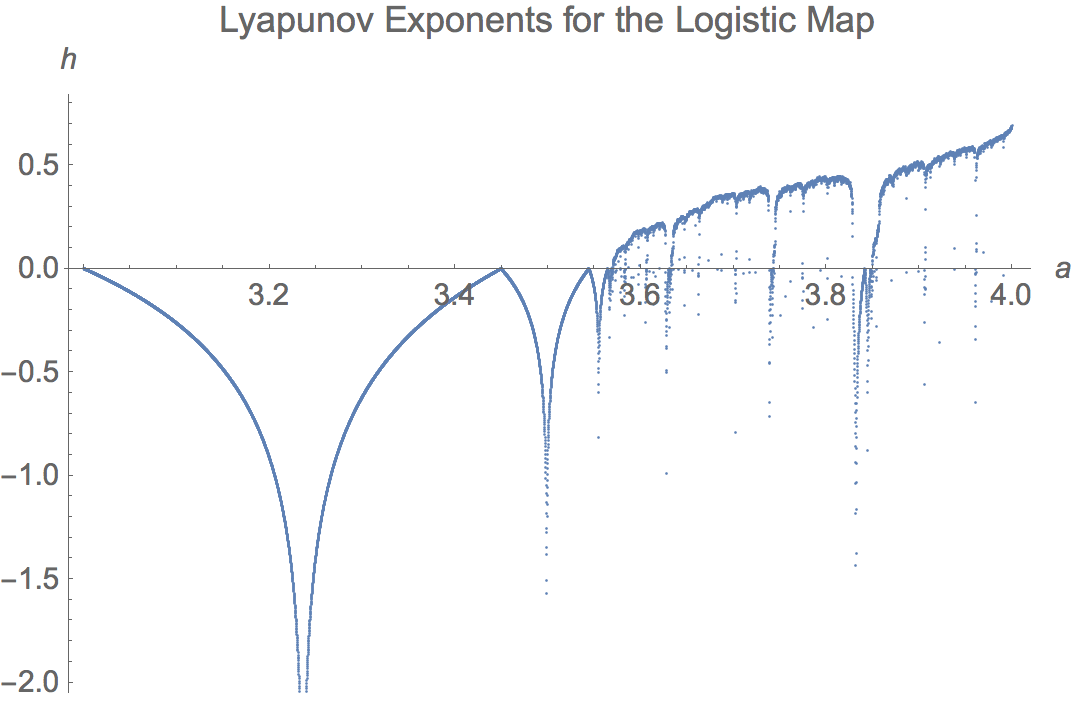
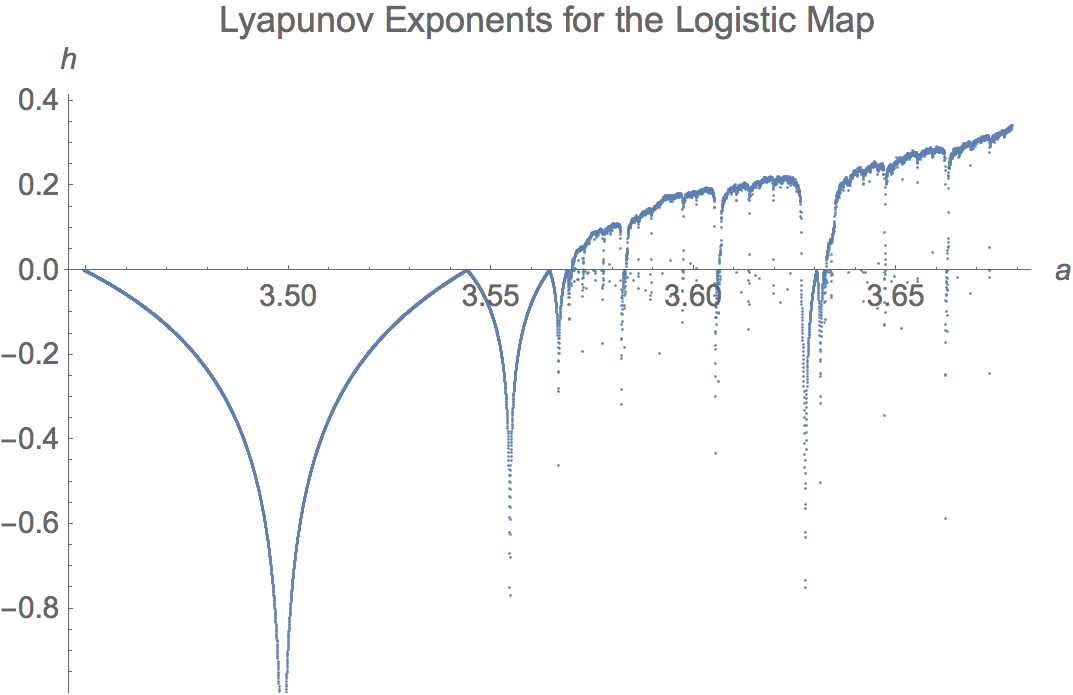
Here is an animation of all three, showing the convergence.
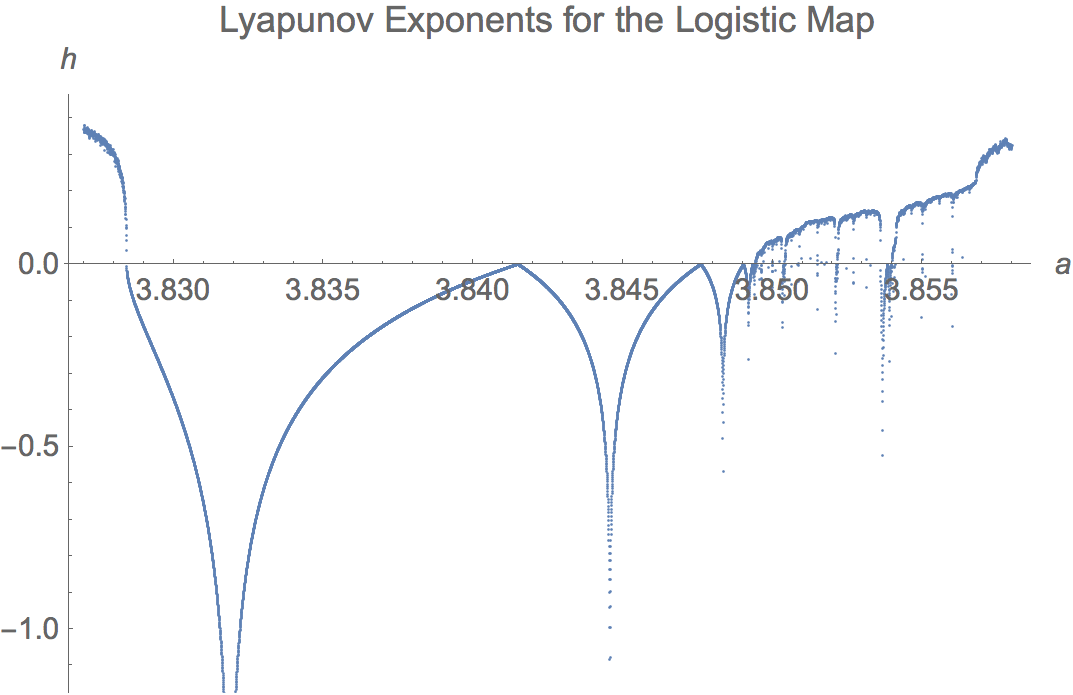
The next figure shows the function in the interval including the so-called period 3 window. It is unknown (at least to me) if the lyapunov number is a continuous function of a. Every periodic window in parameter space has a similar looking graph, but the windows become unimaginably narrow for large periods.