The Lorenz Attractor, Prof. Swift

The Lorenz Attractor

The Lorenz equations are

dx/dt = sigma (y-x)

dy/dt = rho x - y - x z

dz/dt = -beta z + x y

Here are some pictures of the Lorenz atractor, at the classical parameter values of sigma = 10, rho = 28, and beta = 8/3.
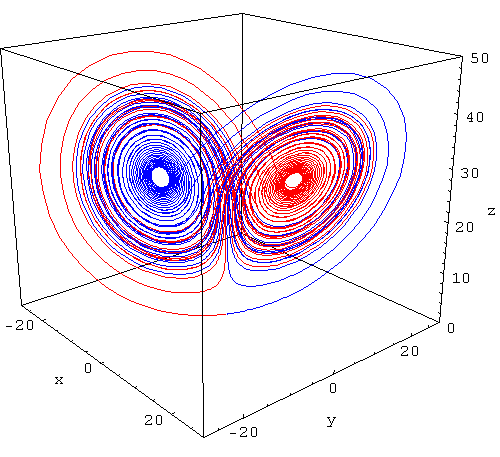
The first figure shows the two braches of the unstable manifold, one in red and one in blue. If you click on the figure, you will see an animation (531 K) where the figure rotates. To make this animate gif smaller, the figure only rotates 180 degrees. This has the effect of switching the colors instantaneoudly every time we loop back to the beginning.

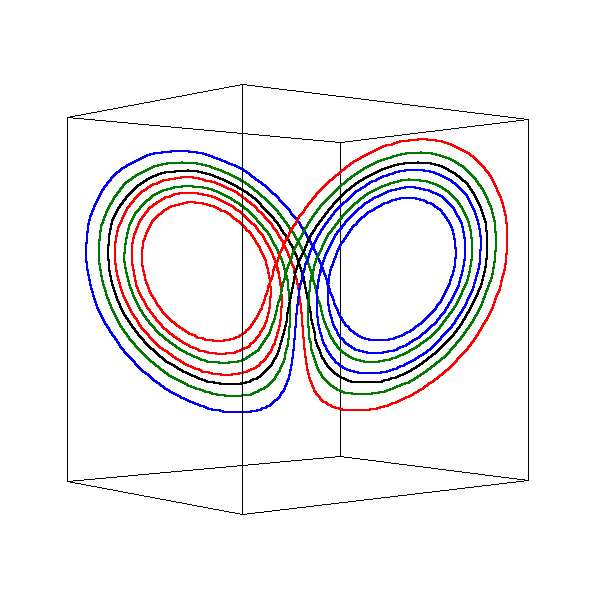
This second figure shows the periodic orbits of type LR (black), LLRR (green), LLLR (red), and RRRL (blue). If you click on this figure, you will see an animation (442 K) where the attractor tilts down. These periodic orbits are all unstable. In fact, unstable periodic orbits are dense in the Lorenz attractor, but there are no stable periodic orbits.

Poincare Map for the Sequence of L's and Rs

This Mathematica Notebook, LorenzPoincareMap can be used to generate a sequence of -1s and 1s depending on whether the trajectory loops left or right. This can be used as a starting point for a class project.

Finding periodic orbits in the Lorenz Attractor

Here is a cdf of the banner image at the math department site. This shows two periodic orbits: L⁹R and R⁹L. Here is the Mathematica notebook that produced that image.

MAT 667 Home page Instructor Information Jim Swift's home page Department of Mathematics NAU Home Page
e-mail: Jim.Swift@nau.edu