Pencils of Curves

Pencils of Curves

[pencil cone]
Note: To view these figures, you need a PC (or PC emulator) running the free DPGraphViewer (or the moderately priced DPGraph) available at DPGraph.

This page is joint work with Michael Falk.

Suppose f(x, y, z) and g(x, y, z) are both homogeneous polynomials of the same degree. Then

α f(x, y, z) + β g(x, y, z) = 0
is a called a pencil of curves.

This page shows 4 different pencils. In each case there are 3 different ways of visualizing the pencil

cos(θ) f(x, y, z) + sin(θ) g(x, y, z) = 0

arrangement_2d shows a 2-dimensional animation were θ increases with time by the formula

θ = (time - sin(time))/8
This has the effect of crossing the interesting angles, θ = n π/4, with zero speed. You see colors because a thin slice of the 3d surface is shown: The part above z = 1 is red and the part below z = 1 is blue. The black curves are lines that appear at special values of θ. These are hyperplanes in 3d, and this arrangement of hyperplanes is what gives each pencil its name.

arrangement_3d shows the 3-dimensional animation.

arrangement_3d_no_planes is a 3-dimensional animation without the planes of the singular curves.

To understand the pencil, ``2d'' is probably the best. The prettiest pictures are obtained with ``3d_no_planes.''

The arrangements are:

Braid arrangement (or A3, or tetrahedron)
f(x, y, z) = x2 - z2 and g(x, y, z) = f(y, x, z)
braid_2d     braid_3d     braid_3d_no_planes
To see the DPGraph figure, click on the link. To get back to this page, exit DPGraph.

Cube arrangement (or B3)
f(x, y, z) = y2 ( x2 - z2) and g(x, y, z) = f(y, x, z)
cube_2d     cube_3d     cube_3d_no_planes

Terao-Falk arrangement
f(x, y, z) = ( x2 - z2)( 9 y2 - z2) and g(x, y, z) = f(y, x, z)
TF_2d     TF_3d     TF_3d_no_planes (This is the graph featured at the top of the page.)

Pappus arrangement
f(x, y, z) = (y-z)(2y+x+z)(2y-x+z) and g(x, y, z) = f(x, y, -z)
Pappus_2d     Pappus_3d     Pappus_3d_no_planes

Here's a series of stills from the "featured" graph, TF_3d_no_planes.


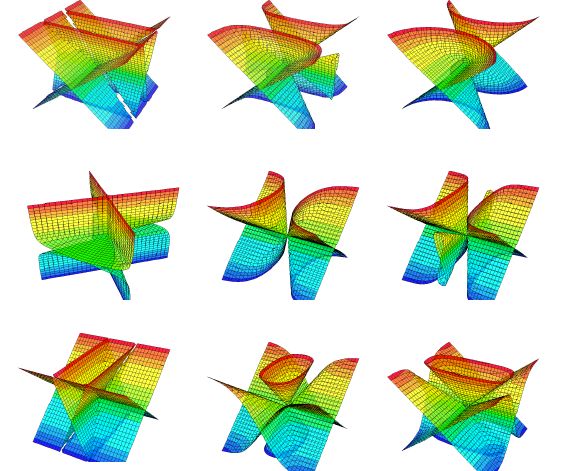
These graphs were produced by DPGraph, which is a fast program for viewing 3D objects.

Jim Swift's DPGraph page     Jim Swift's home page     Department of Mathematics     NAU
e-mail: Jim.Swift@nau.edu