Overflow Map - Ashwin's Figure 2(b)

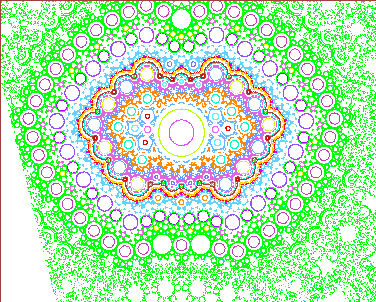
This is an exploration of figure 2(d) in ``Non-smooth invariant circles in digital overflow oscillations'' by Peter Ashwin, NDES 96. For more informations see the list of publications at his web site .

Window: -1.018 < xx < -0.9805,  0.05 < y < 0.08, 
           where xx = 1 - a/2 y.

This is the smallest xx-y rectangle that includes Pete's fig. 2b and 2d. That figure fits in a rhombus that extends to the upper-left and lower-right corners of this figure.
Most of the initial conditions and length of orbits were not recorded, with the exception of the green orbit that ranges over the whole rhombus. You can see the denser region in which the orbit was stayed near the island before it ``escaped''. That green orbit has initial condition (-1, .5105) and is more than 60 million iterations long.
Pete's non-smooth invariant curve, initial condition (b) in the paper, is a red orbit, sandwiched between cyan (light blue) outside and orange inside. This is better seen in the full sized picture obtained by clicking on the figure.
This island is an iterate of the Central Island that is at the corner of the rhombus.

Overflow map page

Jim Swift's home page

Department of Mathematics

NAU Home Page