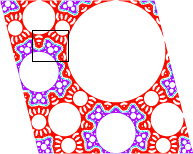
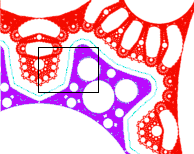
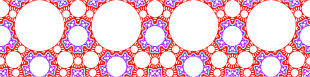
This area preserving discontinuous map of the torus (or rhombus) is
x' = y y' = -x + a y (mod 1)In the figures on this site, a = 0.5. The `mod 1' adds an integer to put the point in the interval [0, 1). If x and y are put in the symmetric interval [-1, 1), the map is called the `lossless digital filter with two's complement overflow' by electrical engineers, or simply the overflow map.
The figures show 3 trajectories of the map with a = 0.5.
Click on one of the icons to see a larger version of the figure.
![[Back]](image/back.gif){kind=small}
Jim Swift's home page
Department of Mathematics
NAU Home Page