The Overflow Map

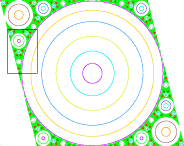
This area preserving discontinuous map of the torus (or rhombus) is

x' =  y
y' = -x + a y (mod 2)

In the figures on this site, a = 0.5. The `mod 2' adds an even integer to put the point in the interval [-1, 1). For more information see ``Non-smooth invariant circles in digital overflow oscillations'' by Peter Ashwin.
A similar map where x and y are in the interval [0, 1) is called the doily map.
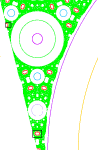
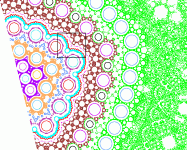
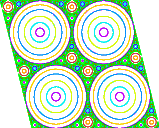
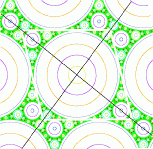
The figures show several trajectories with a = 0.5. The horizontal coordinate is x - a/2 y, and the vertical coordinate is y. If one were to plot y vs. x, the circles would be ellipses.
Click on one of the icons to see a larger version of the figure.

Jim Swift's home page

Department of Mathematics

NAU Home Page